
In this project, I worked on re-implementing key components of the "Pyramid-Based Texture Analysis/Texture" paper, focusing on creating textures that not only match the source image’s appearance but also its structural orientation. The paper introduces a modified Laplacian pyramid, which decomposes an image into frequency bands and orientations in the frequency domain. This decomposition can be visualized as splitting frequency domain amplitudes into circular frequency bands and quadrants. By leveraging histogram matching within these frequency and orientation bands, the algorithm synthesizes textures that capture both the pixel-level characteristics and the overall structural patterns of the source image.
The goal was to replicate the paper's methodology and generate 2D textures that mimic the source texture’s properties. This involved extending previous implementations of the Laplacian pyramid to account for orientation bands and implementing the texture synthesis algorithm as described in the paper’s pseudocode. The process uses histogram matching not only between the source and noisy images but also within the oriented Laplacian pyramid representation. This ensures that the synthesized texture retains the source image's structural coherence and not just its pixel intensity distribution.
The result is a texture synthesis approach capable of producing realistic and structured textures, demonstrating how frequency domain analysis and orientation-based decomposition can elevate texture generation from simple pixel similarity to pattern-aware replication. This project underscores the power of pyramid-based texture analysis in creating compelling, structured textures.
To begin, I utilized the oriented filters discussed in the paper, which play a crucial role in decomposing images into frequency bands and orientations. While many implementations and the original steerable filters paper define these filters in the frequency domain, I opted for a simpler approach by using filters defined in the spatial domain. For this, I leveraged pre-calculated oriented filters available in the pyrtools library, a Python library for pyramid-based image processing.
Although the oriented filters were sourced from pyrtools for convenience, the core of the task required implementing the steerable pyramid independently. This implementation involved decomposing an image into a multi-scale, multi-orientation representation, where each level and orientation captures distinct frequency and directional information. These oriented filters were used as the foundation for constructing the steerable pyramid, adhering to the principles described in the paper.
This step set the stage for further development in the project, including histogram matching and texture synthesis, while ensuring the underlying decomposition process was consistent with the methodology proposed in the paper.

After aligning the oriented filters, the next step was to implement the oriented pyramid, an extension of the Laplacian pyramid. The oriented pyramid construction follows the diagram and methodology outlined in the paper, where each level of the pyramid captures specific frequency and orientation information.
The process begins with constructing a single Laplacian layer, which decomposes the image into its high-frequency details and a lower-frequency residual. The low-frequency component is then further decomposed recursively using the oriented pyramid. This involves applying the pre-calculated oriented filters to split the low-frequency component into multiple orientation-specific bands, each capturing texture and structure at a particular direction.
This recursive decomposition ensures that the pyramid captures multi-scale, multi-orientation representations of the image, making it ideal for texture synthesis and analysis tasks. By closely following the paper's approach, I successfully implemented the oriented pyramid, forming the foundation for advanced histogram matching and texture generation in subsequent steps.
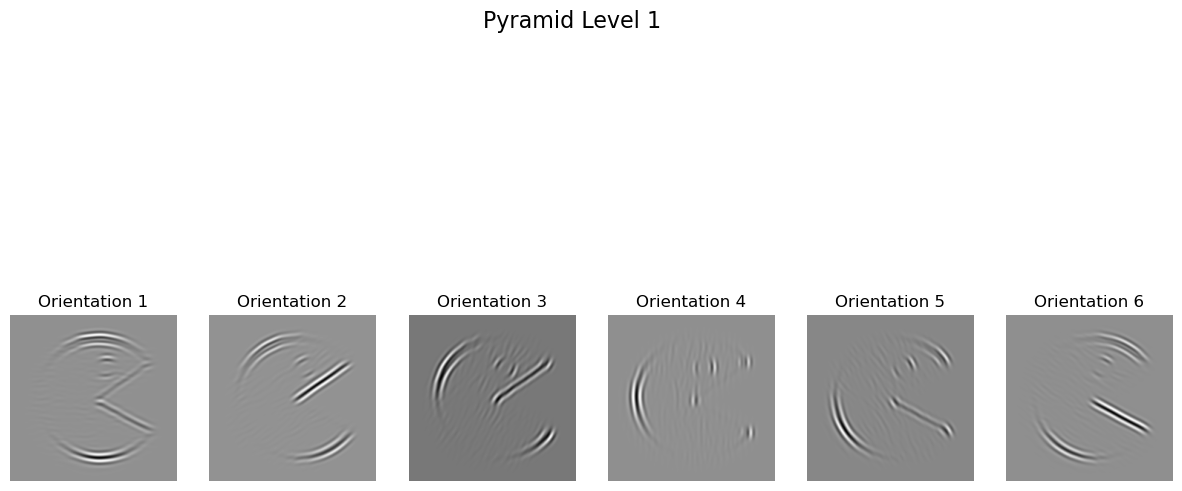
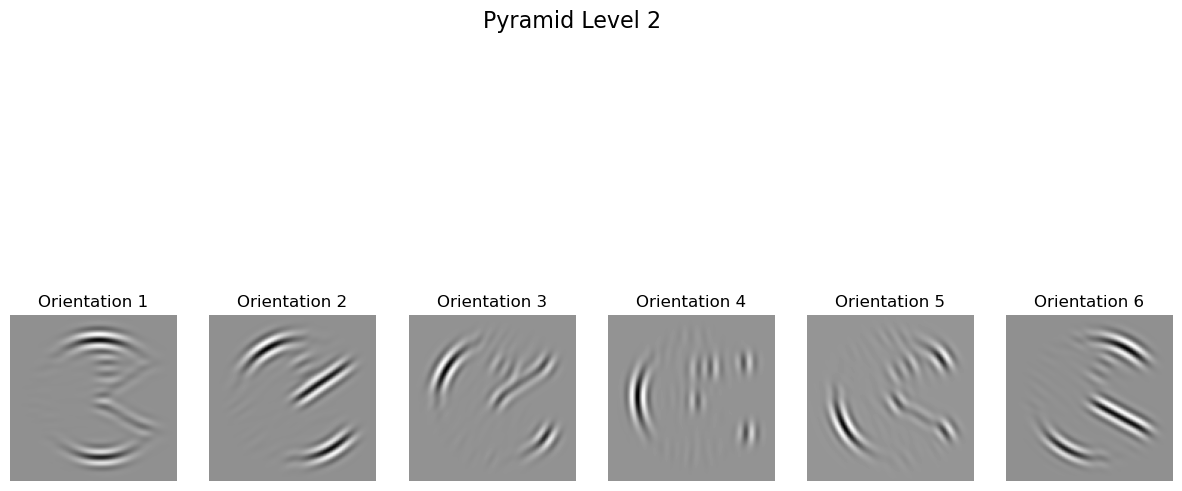

With the oriented pyramid successfully constructed, the next critical step was implementing histogram matching, referred to as match-histogram in the paper. This step ensures that the statistical distribution of pixel intensities in a synthesized texture matches that of the source image, preserving its characteristic appearance and structure. The algorithm, detailed in the paper's pseudocode, involves iteratively adjusting the histograms of the synthesized image to align with those of the source image across all levels and orientations of the pyramid.
To validate this implementation, I performed unit testing on this function and previous components to ensure their correctness and compatibility. A key validation step involved applying the histogram matching process to randomly initialized Gaussian noise, verifying that its histogram converged to match that of a chosen source image. Additionally, I tested the behavior of the oriented Laplacian pyramid to confirm its alignment with the expected results demonstrated in the paper, particularly the pac-man-like example in Figure 4.
By thoroughly testing and verifying these components, I ensured that the histogram matching function integrated seamlessly with the oriented pyramid, setting the stage for successful texture synthesis that faithfully replicates the source image’s properties.



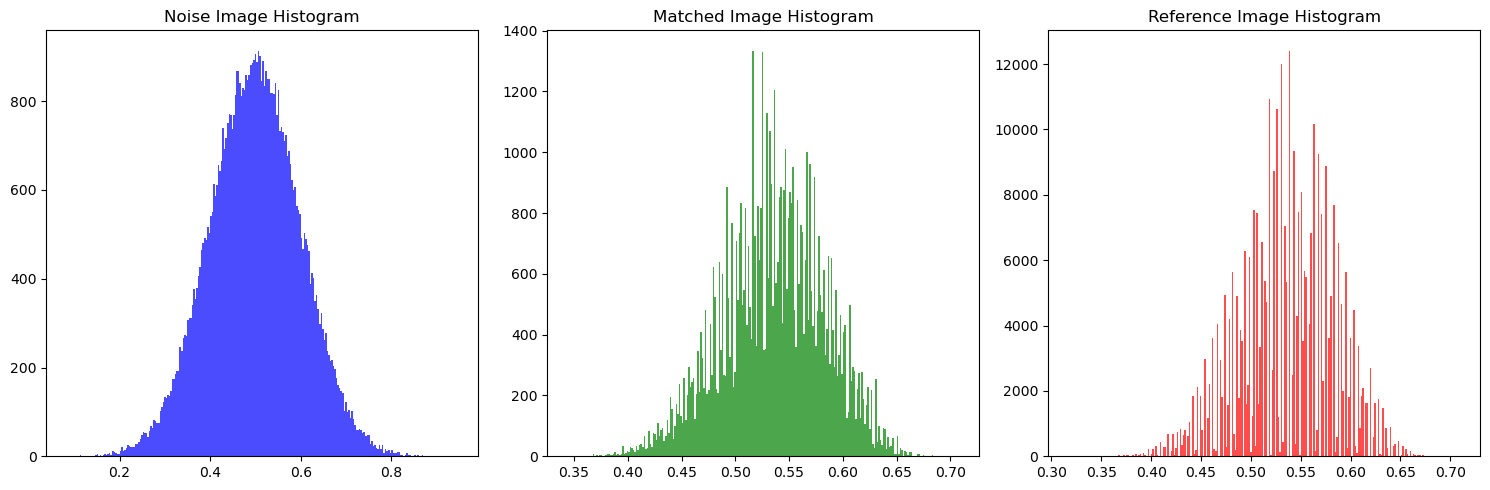
The implementation of the texture synthesis algorithm, named match-texture, marked the culmination of earlier work in this project, integrating all components to create realistic and coherent textures. The algorithm utilized convolution operations and iterative refinement to match feature statistics between the source and synthesized textures. Careful attention was given to practical details such as padding during convolutions, where same or wrap padding ensured seamless edges, avoiding unwanted artifacts and maintaining visual consistency throughout the texture.
A key challenge was handling color images, which required transforming their 3-dimensional RGB pixel values into a PCA basis. This transformation de-correlated and normalized the pixel values, enabling independent operations on the RGB channels. By doing so, the synthesis algorithm could effectively capture and reproduce the complex color patterns present in the source texture. This preprocessing step was implemented with precision to avoid numerical instabilities, ensuring the quality and accuracy of the output.
In conclusion, the texture synthesis algorithm successfully generated high-quality textures that retained the statistical and visual essence of the source image. The integration of PCA for color images and the use of appropriate padding strategies were critical to its success. This work demonstrated the effective application of computational techniques to solve practical problems in texture synthesis and image processing, achieving a balance between computational efficiency and output quality.